12. Recursion¶
What Is Recursion¶
Recursion means “defining something in terms of itself” usually at some smaller scale, perhaps multiple times, to achieve your objective.
Example: $$f(n) = \begin{cases} 1, & \text{if $n$ = 1} \\ f(n-1) + n, & \text{if $n$ > 1} \end{cases} $$
Generally recursion means functions call themselves to solve smaller subproblems.
Calculating the Sum of a List of Numbers¶
Suppose that you want to calculate the sum of a list of numbers such as:
[1,3,5,7,9]
An iterative solution
def listsum(numList):
theSum = 0
for i in numList:
theSum = theSum + i
return theSum
print(listsum([1,3,5,7,9]))
An Recursion solution
$$ \text{lsum(lst)} = \begin{cases} 0, & \text{ lst == [] } \\ \text{lst[0] + lsum(lst[1:])}, & \text{ lst != []} \end{cases} $$def listsum(numList):
if len(numList) == 0:
return 0
else:
return numList[0] + listsum(numList[1:])
print(listsum([1,3,5,7,9]))
Recursive calls
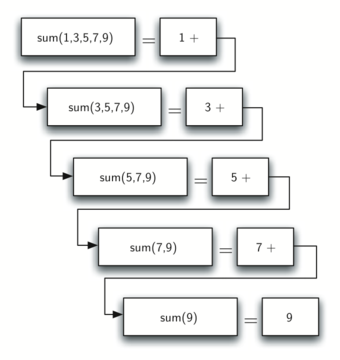
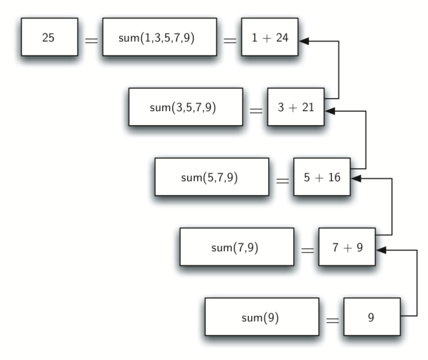
The Three Laws of Recursion¶
Like the robots of Asimov, all recursive algorithms must obey three important laws:
- A recursive algorithm must have a base case.
- A recursive algorithm must change its state and move toward the base case.
- A recursive algorithm must call itself, recursively.
Case: Converting an Integer to a String in Any Base¶
Suppose you want to convert an integer to a string in some base between binary and hexadecimal.
For example, convert the integer 10 to its string representation in decimal as "10", or to its string representation in binary as "1010".
The overall algorithm:
- Reduce the original number to a series of single-digit numbers.
- Convert the single digit-number to a string.
- Concatenate the single-digit strings together to form the final result.
def toStr(n,base):
if n < base:
return str(n)
else:
return toStr(n//base,base) + str(n%base)
print(toStr(1234,6))
print(toStr(65535,9))
Problem of str(n)
Observe the output of:
print(toStr(65535,16))
Better solution
looking up a conversion table to get the converted string.
def toStr(n,base, table):
if n < base:
return table[n]
else:
return toStr(n//base,base,table) + \
table[n%base]
table = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ"
print(toStr(65535,10,table))
print(toStr(65535,16,table))
print(toStr(65535,32,table))
Case: Fibonacci numbers¶
Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 134, ...
fib(0) = 0
fib(1) = 1
fib(n) = fib(n-1) + fib(n-2) for n >= 2def fib(n):
if n <= 1:
return n
t = fib(n-1) + fib(n-2)
return t
fib(10)
Measuring algorithm efficiency
import time
t0 = time.process_time()
n = 35
result = fib(n)
t1 = time.process_time()
print("fib({0}) = {1}, ({2:.2f} secs)".format(
n, result, t1-t0))
%%timeit
fib(35)
Case: Processing nested number list¶
sum([1, 2, 8])
sum([1, 2, [11, 13], 8])
sum all the numbers in recursive nested number list
def r_sum(nested_num_list):
tot = 0
for element in nested_num_list:
if type(element) == type([]):
tot += r_sum(element)
else:
tot += element
return tot
r_sum([1, 2, [11, 13], 8])
Case: Tower of Hanoi¶

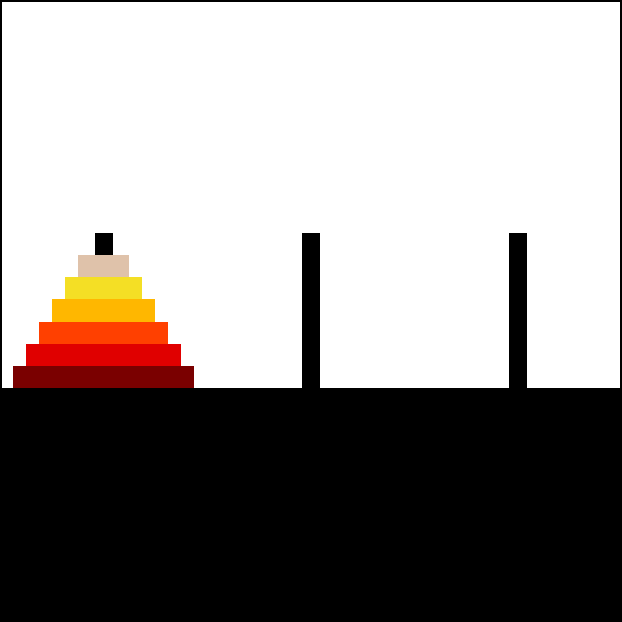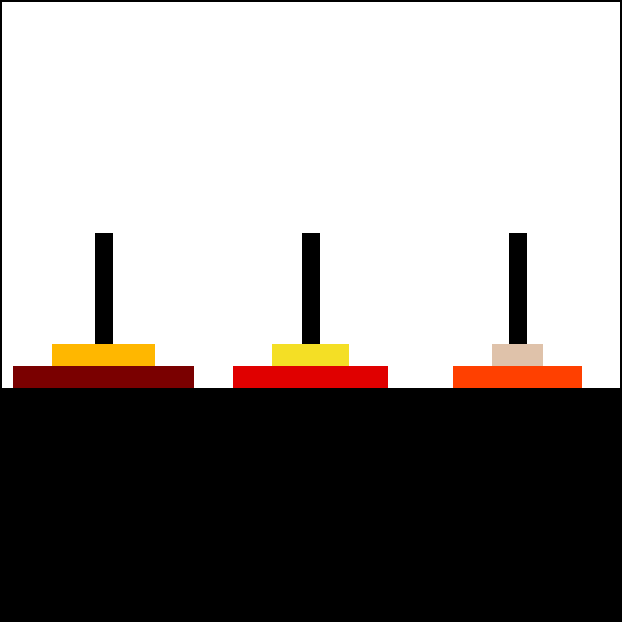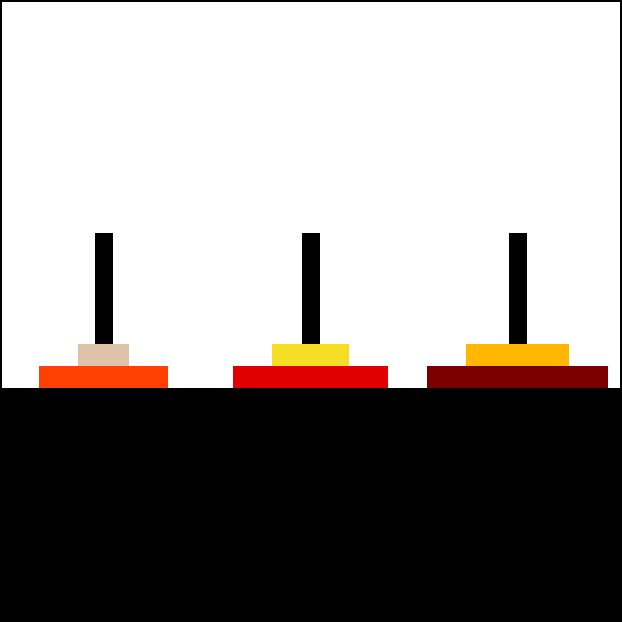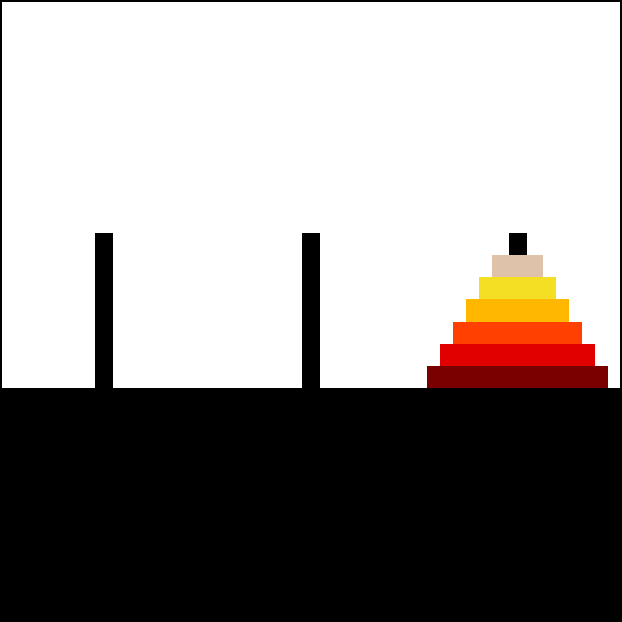
def hanoi(n, a, b, c):
if n > 0:
hanoi(n - 1, a, c, b)
print(n, ':', a, '->', c)
hanoi(n - 1, b, a, c)
hanoi(3, 'A', 'B', 'C')
Eight queens puzzle¶
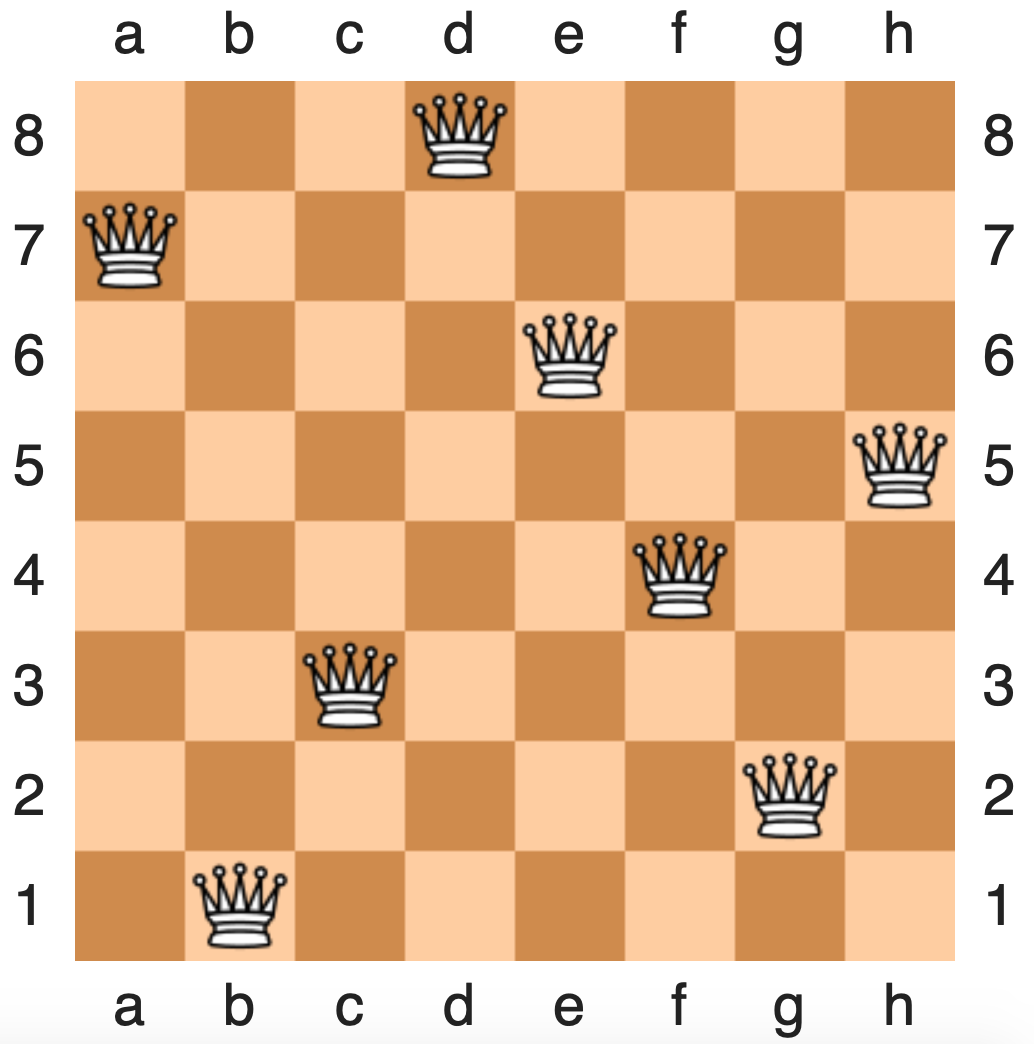
def conflict(row, col, queens):
for pr in range(row):
if queens[pr] == col or abs(col - queens[pr]) == row - pr:
return True
return False
def queen(ans, row=0):
if row == len(ans):
print(ans)
else:
for col in range(len(ans)):
if not conflict(row, col, ans):
ans[row] = col
queen(ans, row+1)
queen([None]*8)
def conflict(row, col, queens):
for pr in range(row):
if queens[pr] == col or abs(col - queens[pr]) == row - pr:
return True
return False
def queen(ans, row=0, alls=[]):
if row == len(ans):
alls.extend([ans[:]])
else:
for col in range(len(ans)):
if not conflict(row, col, ans):
ans[row] = col
queen(ans, row+1, alls)
ans = []
queen([None]*8,0, ans)
print(len(ans), ans)
SIZE = 8
def conflict(col, queens):
left = right = col
for c in reversed(queens):
left, right = left-1, right+1
if c in (left, col, right):
return True
return False
def queen(n):
if n == 0:
return [[]]
parts = queen(n-1)
return [solution+[i]
for i in range(SIZE)
for solution in parts
if not conflict(i, solution)]
ans = queen(SIZE)
print(len(ans))
for answer in ans:
print(answer)
SIZE = 8
def conflict(col, queens):
left = right = col
for c in reversed(queens):
left, right = left-1, right+1
if c in (left, col, right):
return True
return False
def queen(n):
if n == 0:
return [[]]
parts = queen(n-1)
ans = []
for solution in parts:
for i in range(SIZE):
if not conflict(i, solution):
ans.append(solution+[i])
return ans
ans = queen(SIZE)
print(len(ans))
for answer in ans:
print(answer)
Limited Recursion Depth
>>> import sys
>>> sys.getrecursionlimit()
>>> 3000
Improve efficiency
import functools
@functools.lru_cache(maxsize=None)
def fib(n):
if n <= 1:
return n
t = fib(n-1) + fib(n-2)
return t
print(fib(200))
print(fib.cache_info())
import functools
# the minimal cache size for fibonacci ?
@functools.lru_cache(maxsize=3)
def fib(n):
if n <= 1:
return n
t = fib(n-1) + fib(n-2)
return t
print(fib(200))
print(fib.cache_info())
Exercise: Write a function to implement the Pascal's triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1def pascal(n):
if n == 1:
return [1]
else:
line = [1]
p_line = pascal(n-1)
line = [ p_line[i]+p_line[i+1] for i in range(len(p_line)-1)]
line.insert(0,1)
line.append(1)
return line
pascal(6)
def pascal(n):
if n == 1:
return [[1]]
else:
line = [1]
p_lines = pascal(n-1)
return p_lines + [[1] + [ p_lines[-1][i]+p_lines[-1][i+1]
for i in range(len(p_lines[-1])-1)] + [1]]
pascal(6)
How to print Pascal's triangle on screen?
Exercise: Coin Change Problem
Given a value V, if we want to make change for V cents, and we have infinite supply of each of C = { C1, C2, .. , Cm} valued coins. Find all the possible solutions.
def change(m, changes):
if m == 0:
return [[]]
ans = []
for c in changes:
if m-c >= 0:
parts = change(m-c,changes)
for part in parts:
part.append(c)
ans.extend(parts)
return ans
ans = change(10,(10,5,2,1))
for i in ans:
print(i)
def change(m, changes):
if m == 0:
return [[]]
ans = []
for c in changes:
if m-c >= 0:
parts = change(m-c,changes)
for part in parts:
part.append(c)
ans.extend(parts)
return ans
ans = change(10,(10,5,2,1))
newans = set([tuple(sorted(i)) for i in ans])
for i in newans:
print(i)
Exercise: Stairs problem
There are N stairs, a man can go up 1,2 or 3 stairs in each step. Count all the possible step solutions.
def step(n, s):
if n == 0:
return [[]]
ans = []
for i in s :
if n-i >= 0 :
ans.extend([p+[i] for p in step(n-i,s)])
return ans
ans = step(4,{1,2,3})
print(ans)
Glossary¶
base case
A branch of the conditional statement in a recursive function that does not give rise to further recursive calls.
infinite recursion
A function that calls itself recursively without ever reaching the base case. Eventually, an infinite recursion causes a runtime error.
recursion
The process of calling the function that is already executing.
recursive call
The statement that calls an already executing function. Recursion can even be indirect — function f can call g which calls h, and h could make a call back to f.
recursive definition
A definition which defines something in terms of itself. To be useful it must include base cases which are not recursive. In this way it differs from a circular definition. Recursive definitions often provide an elegant way to express complex data structures.